LA FRÉQUENCE D’UN SON
Le son est perçu par l'homme lorsque son oreille est soumise à une alternance de compressions et d'expansions de l'air ambiant. Pour qu'il soit possible d'entendre quelque chose, il faut que ces alternances aient lieu entre vingt fois par seconde pour les sons les plus graves et vingt mille fois par seconde pour ceux plus aiguës.
Cette plage de fréquence explique, par exemple, que certains cris de chauves-souris ne soient pas entendus, parce que se positionnant à des hauteurs trop aiguës pour nos chères oreilles.
Précisons naturellement que ces variations de pression sont toujours produites par un corps en vibration. Ce corps peut être une corde tendue, une lame de métal, une membrane ou tout autre système utilisé par des instruments de musique.
L’EXPÉRIENCE DE LA LAME MISE EN VIBRATION
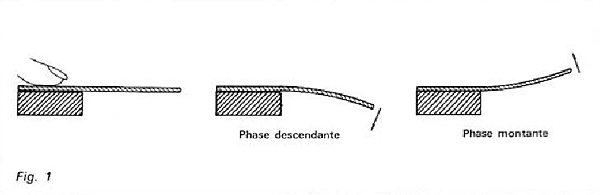
Avant toute chose, nous allons considérer un système oscillant que tout le monde a dû expérimenter un jour ou l'autre. Il s'agit d'une lame de métal (genre lime à ongles) que l'on coince sur le bord d'une table.
En position de repos, la lame est inerte, stable, et se trouve en position horizontale. Si nous lui appliquons une certaine force vers le bas, une contre-force va tendre à lui redonner sa position d'équilibre. La lame repart dans l'autre sens avec une vitesse allant en accélérant jusqu'au point de repos où il n'y aura plus de contre-force, mais où la vitesse aura atteint son maximum. Puis la lame continue sur sa lancée jusqu'à un point symétriquement opposé au premier (le haut) où la vitesse sera nulle, mais la contre-force à son maximum. Ensuite, la lame repart dans l'autre sens, vers le bas.
© Sono
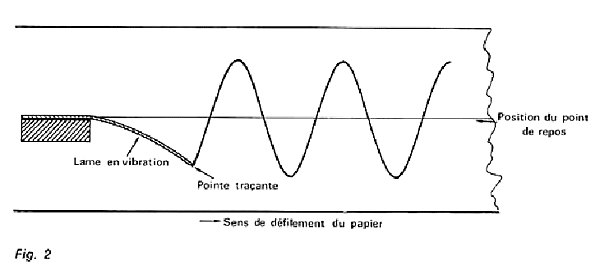
Ce petit manège pourrait durer éternellement s'il n'existait pas certaines gênes naturelles, du genre frottement de l'air, pour freiner et stopper le mouvement. S'il était possible de fixer une pointe traçante au bout de la lame et de dessiner le chemin qu'elle parcourt sur une bande de papier défilant à son contact, nous obtiendrions une courbe dont l'amplitude irait en décroissant.
© Sono
LE CYCLE DE VIBRATION
Un cycle de vibration est une excursion complète de la pointe entre le moment où la lame se trouve au point de repos et le moment où elle y revient de nouveau, après être passée par les deux maxima haut et bas. La moitié de la distance verticale entre ces deux maxima est appelée amplitude du signal et le nombre de cycles complets en une seconde est appelé fréquence.
Le temps nécessaire à la durée d'un cycle est appelé période. Par exemple, un cycle présentant une période d'un millième de seconde correspond à une fréquence de mille cycles par seconde : on dit mille hertz (Hz) ou un kilohertz (kHz). Par son mouvement, la lame produit des variations de la pression de l'air à une certaine fréquence, une certaine amplitude et pendant un certain temps au cours duquel l'amplitude va varier.
Toutes ces notions vont servir à définir les premières indications d'un son.
- La fréquence : sa hauteur.
- L'amplitude : son volume.
- Le temps : sa durée, ainsi que les variations de fréquence et d'amplitude durant la durée de ce son.
Cependant, il ne faudrait surtout pas oublier une quatrième composante fondamentale entrant dans la définition du son : le timbre. Celui-ci conditionne la couleur sonore qui sert ainsi à déterminer l'origine instrumentale d’un son. Dit autrement, c’est ce qui fait qu’une flûte et une trompette jouant une même note (fréquence, amplitude et durée) sonneront différemment.
Toutes ces notions physiques, essentielles à la constitution d’un son, s'apparentent à des réalités musicales et s'appliquent également à la conception du matériel musical sonore et à la lutherie électronique.
LÀ OÙ IL EST QUESTION DE HAUTEUR, D’INTERVALLES ET DE GAMMES
On a dit que la hauteur d'une note en musique, correspond à sa fréquence en acoustique. Cependant, en musique, chaque note possède sa fréquence officielle, calculée à partir du La, troisième octave, qui sonne à 440 Hz (le La du diapason). Ce n'est que depuis l'apparition de la lutherie électronique que l'on utilise des fréquences intermédiaires. Du reste, les instruments, à part le violon, n'étaient pas prévus pour.
Les gammes que nous utilisons encore de nos jours datent de la Grèce antique. Le premier intervalle utilisé est l'octave, qui est le plus juste. Si nous mesurons les fréquences des “La” situés de part et d'autre du La 440 Hz, celui qui est au-dessus fait 880 Hz, c'est-à-dire le double, et celui qui est au-dessous fait 220 Hz, donc la moitié. Ainsi, un intervalle d'octave correspond à un rapport de fréquence de un à deux.
Ensuite, si nous considèrons la quinte comme l'intervalle le plus juste après l'octave, le rapport de fréquence obtenu est de 4/2. Par exemple, pour un La situé à 220 Hz, l'octave est de 440 Hz et la quinte supérieure à l'octave de 660 Hz (Mi). Si on divise par deux on obtient, de La à Mi, une quinte entre 220 et 330 Hz, avec un rapport 3/2.
Si l'octave a servi aux Grecs à déterminer l'intervalle de base dans lequel se situerait la gamme (majeure), la quinte est l'intervalle essentiel pour obtenir les degrés de cette gamme. En effet, si on part du Faet que l'on monte vers l'aigu d'une quinte, on arrive à Do, puis en continuant par saut de quintes, nous obtenons : Do à Sol, Sol à Ré, Ré à La, La à Mi et Mi à Si. En regroupant toutes ces notes à l’intérieur d'une même octave, nous obtenons la gamme majeure bien connue : do, ré, mi, fa, sol, la, si.
Le troisième intervalle, juste à l'oreille, est la quarte et il présente un rapport de 11/8. La quarte du "La 440 Hz", c'est-à-dire le Ré, fait environ 600 Hz. En outre, on s'aperçoit qu'une quarte représente le complément de la quinte dans l'octave. De Do à Sol, il y a une quinte, et de Sol à Do, il y a une quarte.
Toute la musique occidentale et une partie non négligeable des musiques extra-européennes sont basées sur ces trois intervalles. Il n’y a qu'à regarder comment est construit un blues classique pour voir que la grille harmonique se contente des accords de tonique, de quarte et de quinte. Du reste, les anciens avaient remarqué ce rapport mathématique entre les fréquences des notes en harmonie, non pas en comptant leur nombre de cycles par seconde, car cela ne leur était pas techniquement réalisable, mais en mesurant la longueur des tuyaux de la flûte de pan ou des cordes de la lyre misent en vibration.
DE L’IMPORTANCE DE LA LONGUEUR ET DE LA TENSION POUR ACCORDER
Les fabricants d'orgues électroniques définissent le registre des jeux de l'instrument en mentionnant les pieds, comme les facteurs d'orgues anciens définissent la fréquence de leurs tuyaux en les mesurant en pieds. Ainsi, un jeu de flûte de huit pieds représente un jeu de tuyaux à sifflets (jeu de fond), dont le plus grave, c'est-à-dire le plus long, mesure huit pieds de haut (NB : le La 440 Hz, troisième octave, trouve sa place naturelle sur le clavier d'orgue, lorsque l'on utilise un jeu de huit pieds).
Par contre, il en va autrement lorsqu'on veut accorder un instrument à cordes, comme la guitare ou le piano. Pour ce faire, il faut jouer sur la tension de la corde. Pour rendre le son de la corde plus aigu, il faut la tendre. Ceci aura pour effet d'augmenter la fréquence. À l'inverse, la détendre diminuera sa fréquence et rendra le son plus grave.
De son côté, le trompettiste, qui ne dispose que de trois pistons pour faire douze notes par octave et plusieurs octaves de registre, est obligé de tendre plus ou moins ses lèvres (pression) quand il veut changer de zone de fréquence.
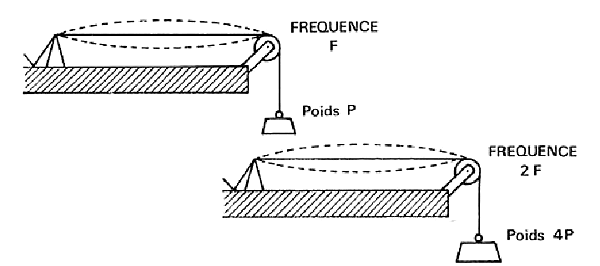
À la figure ci-dessous, on peut voir une illustration de ce phénomène : si, à longueur égale, une corde vibrante quadruple de tension, sa fréquence double et la note produite monte d'une octave. Pour une même corde, la fréquence est proportionnelle à la racine carrée de la tension.
© Sono
À présent, nous avons deux facteurs qui déterminent la fréquence de vibration d'un objet sonore : sa longueur et sa tension. Or, il en existe un troisième que l’on peut observer avec un instrument comme la guitare : les six cordes ont la même longueur, mais pas la même épaisseur. C'est en effet le troisième facteur déterminant la fréquence de l'objet en vibration. Plus cet objet est lourd et dense, plus sa fréquence de résonance est basse. Ce qui s'explique par l'inertie due au poids de la corde lorsque celle-ci se déplace en vibrant.
Sur les pianos et les harpes, il y a deux facteurs pris en considération dans la disposition des cordes : la longueur et l'épaisseur, ce qui permet de tendre toutes les cordes avec la même force et d'ajouter de la solidité et de la rigidité au cadre qui les soutient. (1)
Il est très important de correctement assimiler ce phénomène de vibration et de fréquence pour pouvoir comprendre ce qu'est la notion de timbre qui définit alors sa personnalité.
1. Sur le piano, à partir du registre médium/aigu, les cordes sont doublées puis triplées, ceci pour obtenir un équilibre relatif en termes de puissance sonore sur l'ensemble de la tessiture.
P.-Y. MONFRAIS (Piano Web - 08/2022)
(source : Sono)
À CONSULTER
SON ANALOGIQUE ET SON NUMÉRIQUE, QUELLES DIFFÉRENCES ?
LES CONTOURS DU SON ANALOGIQUE ET NUMÉRIQUE
LE SON ANALOGIQUE EST-IL TOUJOURS UTILE ?



